gps-accuracy

The purpose of this script is to quantify the accuracy of a GPS device by comparing the location of track points against points in the planned route. For details of the use of this script to assess the accuracy of a variety of GPS devices, please see findings.

Usage:

gps-accuracy [-h] [-d] route track

positional arguments:
  route        filename of route (GPX track format)
  track        filename of track (GPX track format)

optional arguments:
  -h, --help   show this help message and exit
  -d, --debug  generate debug output, including a GPX file visualising
               tracking errors

The output reports on the mean, median and 95% percentile distance from each GPX track point to the nearest point along the planned route. It also reports on the start and finish time of the track, the number of trackpoints and the mean/max interval between successive track points.

The core of the algorithm is to find the nearest point on the planned route to each track point. There are two main scenarios:

1. The nearest point along the planned route coincides with a route point. This is typically the case if the route is curving away from the track point under consideration. This is illustrated below, in the case of track point T2, where the error, e, is discovered by locating the nearest of all route points (R3) and simply calculating the Euclidean distance between the two points.

2. The nearest point along the planned route lies somewhere on a line between two successive route points. This is illustrated below in the case of track point T1, where the closest route point lies on the straight line between R1 and R2. The error line, e, is perpendicular to the line segment R1-R2. The point of intersection is found by considering the line R1-R2 as a linear equation y = mx + c, which implies that the slope of the line e must be -1/m. We can solve the resulting pair of simultaneous equations to find a point of intersection, and thus find the error distance, e, which is the Euclidean distance between T1 and the intersection. The complication is that we don’t know which pair of route points present the closest line segment to track point T1. The heuristic method used, is to find the closest route point, R, to track point T, then consider line segments between R and its two predecessors and two successors: (R-2)-(R-1), (R-1)-R, R-(R+1) and (R+1)-(R+2). For each segment, we calculate a point of intersection between the line and its perpendicular through T using the method of simultaneous equations. We eliminate any candidates where the intersection is not between the successive route points (for instance, point T3 to the extended line between R2 and R3) and select from the remaining candidates the shortest error distance.

The following image visualises the errors between a section of the planned route (red) and the recorded track (blue).

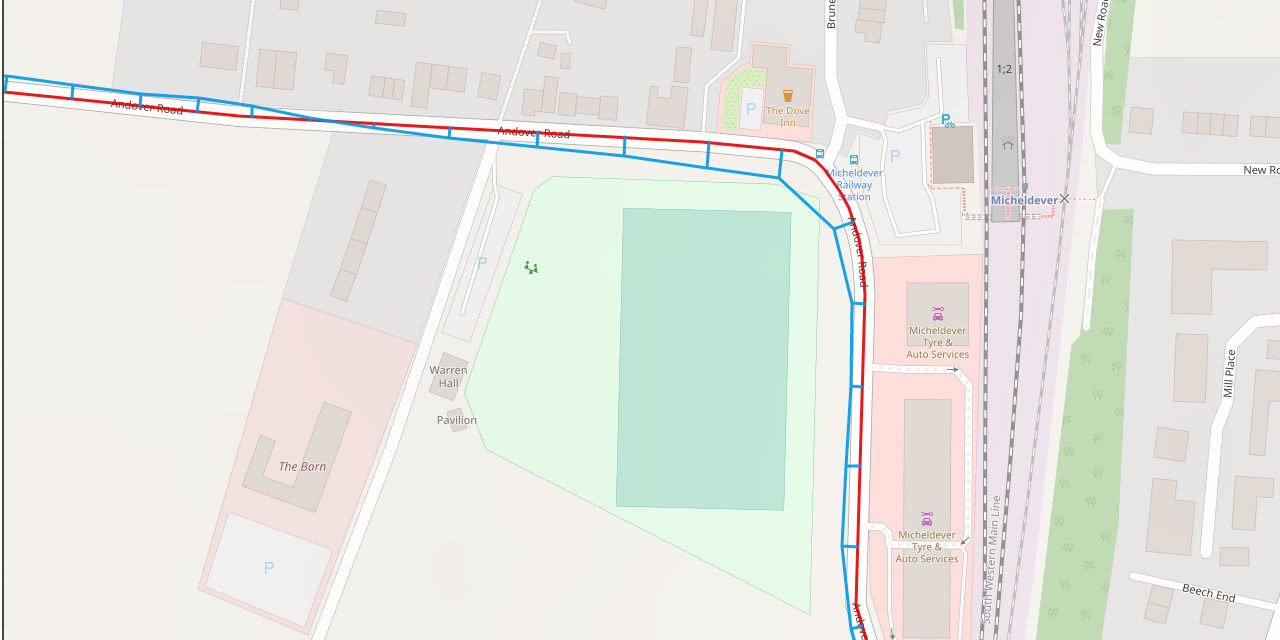
Assumptions

• Trackpoints in the route file are closely-spaced, such that the intended route can be considered to follow a straight line between successive route points.
• Since the distances between points in the route and track are very small, the curvature of the earth can be ignored. The first step is therefore to convert the lat/long coordinates the route and track to XY coordinates (units are metres), and make distance calculations using Pythagoras theorem.
• The base maps used to create the planned route are accurate; specifically that the path of a road as described on the map accurately represents the path of that map in the real world.

This site is open source. Improve this page.